Superconductors

What is a superconductor?

I have noticed that physicists are rarely given to excesses of exuberance in talking about their subject, even among themselves. So when they use a prefix like super for a material, it must be something quite extraordinary. I shall first tell you what the phenomenon is, and then explain why it is extraordinary. Suppose I take a wire of the metal lead which has a resistance of one ohm at room temperature, about 290 K, and measure its electrical resistance at different temperatures as I cool it down. I show the result in fig. 1. The resistance drops smoothly as the temperature drops. Near 7 K, the resistance drops abruptly by a factor of more than 10²⁰ below its value at room temperature, and remains so at all lower temperatures. Put differently, the wire now conducts electric currents at least 10²⁰ times better than it did before. In fact, we can only set an upper limit to this number because of the limits on the sensitivity of the measuring instruments. For all we know, the wire in this condition may be a perfect conductor, which means that a current can pass through it with zero voltage applied to it.

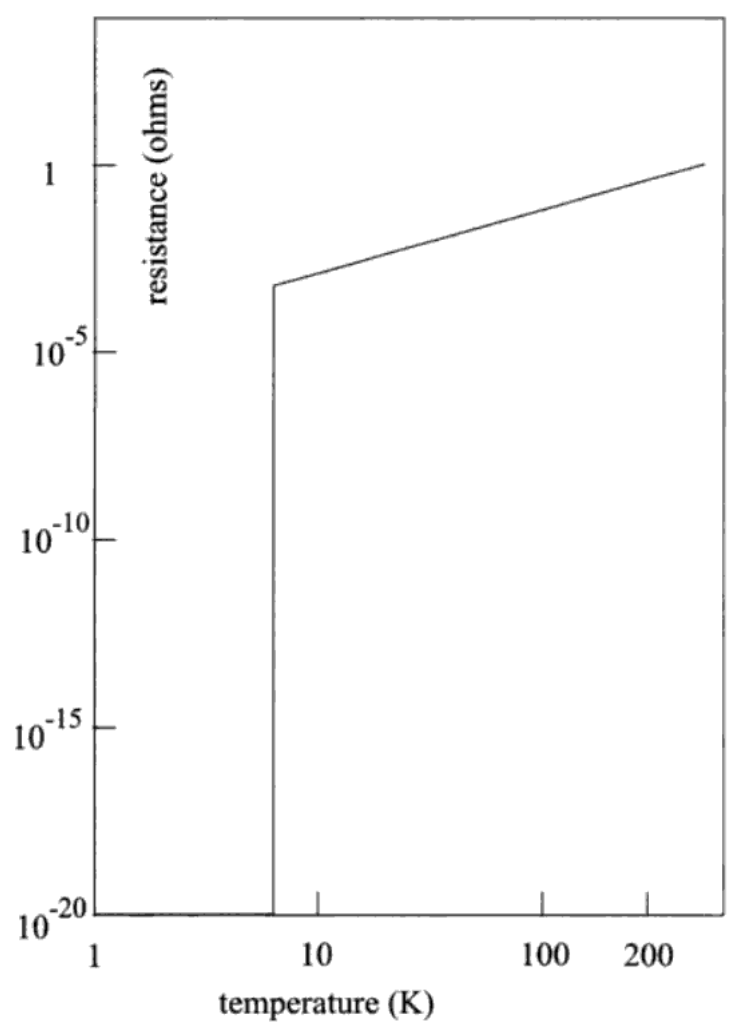
FIGURE 1. Superconductivity of lead metal. Note that the scales are logarithmic, and not linear. This is a convenient way to show the variation of quantities over a large range of values. Thus here the temperature varies by a factor of a few hundred, and the resistance by a factor of 1020. The resistance drops precipitously to zero at a temperature of about 7 K

If I now warm up the lead wire from the superconducting state, I find that its resistance jumps back to its original value at the same temperature at which the resistance had disappeared when cooling the wire. I call this temperature the superconducting transition temperature, and use the symbol T0 (read T-nought) to denote it. When the wire is above this temperature and therefore not superconducting, I say that it is in the normal state. The change from one state to the other is very abrupt: a change of temperature of less than a thousandth of a degree is enough to cause the transition.

We begin to see why superconductivity is so extraordinary. There is the enormous change in the electrical resistivity, and then there is the abruptness (meaning the narrowness of the temperature range) with which it occurs. We saw in chapter IX how electrical resistance arises. It involves interactions between the conduction electrons, phonons, and alloying atoms: a complicated interplay of huge numbers of particles (more than 10²⁰ electrons alone, not to mention the others). This cacophony is abruptly and totally stilled just by cooling the wire a thousandth of a degree through the transition temperature. Something happens which affects the interplay of all these particles, and which dramatically changes their behaviour. Here is an analogy: I hear a din emerging from a classroom, and it suddenly ceases when a bell rings. Subsequent research shows me that the reason for the silence was the entrance of the teacher. So the task is to find out what plays the role of the teacher in superconductivity.

We are accustomed to seeing small changes in properties with small changes in temperature: the thermal expansion of solids, for example. This implies that the fundamental structure of the material, meaning its basic atomic and electronic structure, also undergoes correspondingly small changes. The situation is quite different with superconductivity. The abrupt disappearance of electrical resistance implies that some new feature must have appeared in the superconducting state which just did not exist in the normal state. This is an example of a phase transformation. Ferromagnetism and the melting of solids are other examples of such transformations. They are all characterized by a sudden change in the group (as distinct from individual) behaviour of all the relevant particles in the material: the conduction electrons in a superconductor, the electron magnetic moments in a ferromagnet, the atoms in a solid undergoing melting. Because of the large numbers of particles involved and the complicated interactions among them, it is a formidable challenge to explain them in detail. The effort to do so has been most successful with superconductivity, and I shall describe it later in this chapter.

Superconductivity is, perhaps surprisingly, anything but a rare occurrence in materials. In addition to lead, there are twenty-seven other naturally occurring elements which become superconducting, each with its own characteristic transition temperature. There are hundreds of alloys and compounds which are also superconducting. Superconductivity is a far more widespread phenomenon than ferromagnetism, which appears in only a few materials.

I list in table 1 the transition temperatures of a few superconductors. I have selected them to bring out two points: the variety of materials which can become superconducting, and the great range of transition temperatures. The two extreme temperatures in the table differ by a factor of almost eight thousand.

I should mention here as an aside that in physics, a comparison of two temperatures is often more meaningful in terms of their ratio than their difference. This is because in statistical physics, which is at the heart of the idea of temperature, the ratios of the energies of quantum levels to the thermal energy (which is basically what temperature is) are more significant than the temperature by itself. The percentage change in this ratio is the same in going from, say, one degree to ten degrees, as from a hundred degrees to a thousand degrees.

Table 1. Some superconducting transition temperatures

Tungsten	0,012
Tin	3,7
Lead	7,2
An alloy of niobium and titanium	11,0
A compound of niobium and tin	18,0
A compound of yttrium, barium, copper and oxygen	90

QUESTION. Even though superconductivity is much more prevalent than ferromagnetism, why is it that I see so many uses of magnets around me and none of superconductors?

ANSWER. We have materials which are ferromagnets at ordinary temperatures (around 300 K, say) but none which are superconducting at these temperatures. Any use of superconductors would require refrigeration with liquid air (90 K) or liquid helium (4 K) using special equipment, and this rules out the everyday use of superconductors on a scale anywhere near that of magnets. The search continues for materials which are superconducting at room temperature, so far without success.

Some other properties of superconductors

The disappearance of electrical resistance is the most spectacular property which distinguishes a superconductor from a normal metal. A matter of terminology: I use the term normal in this chapter as synonymous with non-superconducting. Thus lead is normal above 7.2 K, and superconducting below that temperature.

Now imagine that I have the wire of lead sitting at a temperature of around 4 K, which is the same as minus 269 °C. I get to such low temperatures by using liquified helium gas. The wire has an electric current flowing through it but with no voltage, because it is superconducting. Can I do anything to the wire to disturb its superconductivity? Shaking it or shining light on it does nothing. Knowing that electric current is carried by electrons, and that a magnetic field influences their motion, I let a magnet approach the wire. At first nothing happens; the current continues to flow undiminished. But when the strength of the field at the wire has reached some apparently critical level, the current in the wire suddenly drops and a voltage appears: the wire has lost its superconductivity and now shows its normal electrical resistance. I try a few more tests, and find that at each temperature, there is a critical strength of magnetic field, below which the lead wire is superconducting and above which it is normal. I show in fig. 2 how this critical strength varies with temperature, beginning with very small values near T0 and levelling off at a maximum of about 800 gauss at the lowest temperatures. The gauss is the unit in which the strength of a magnetic field is measured. The strength of the earth's field is about half a gauss.

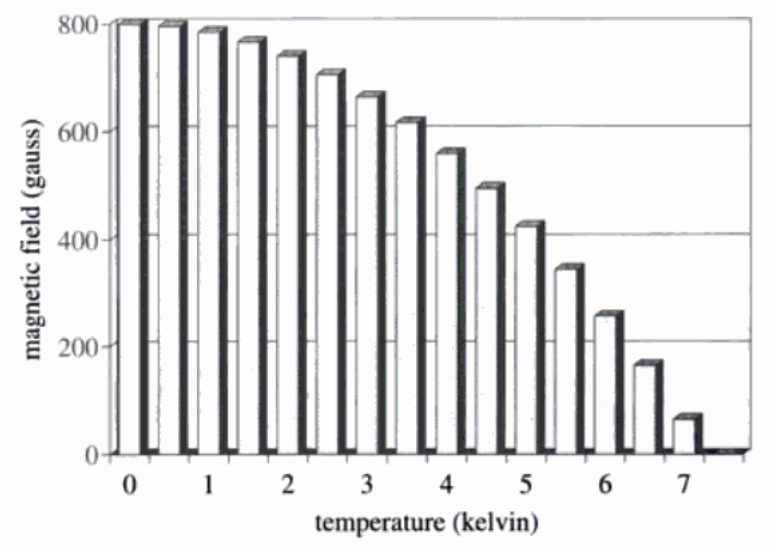
FIGURE 2. The smallest magnetic field (in gauss) which will destroy superconductivity in lead at different temperatures. Fields less than this do not affect the superconductor

Different superconductors show the same qualitative variation of critical field as the temperature is varied, but have different values for this maximum critical field, for which I use the symbol HM. Table 2 lists HM for several superconductors. One sees that superconductors fall into two groups in terms of HM.There are those whose critical fields are a few hundred gauss or less, and then those with fields of hundreds of thousands of gauss. I shall refer to them as the low-field (LF) and the high-field (HF) superconductors respectively. The reason for the different behaviours lies in the details of how the superconductor reacts to a magnetic field, as we shall see now.

Table 2. Maximum field.HM for superconductivity in some materials

Tungsten	1
Tin	3
Lead	800
An alloy of niobium and titanium	120,000
A compound of niobium and tin	300,000
A compound of yttrium, barium, copper and oxygen estimated to be more than	more than 1,000,000

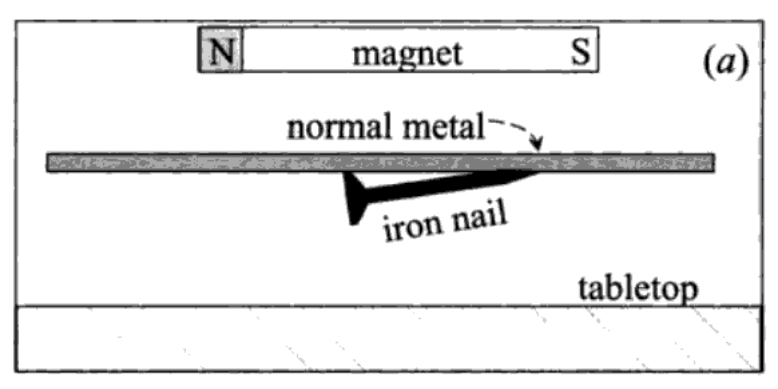
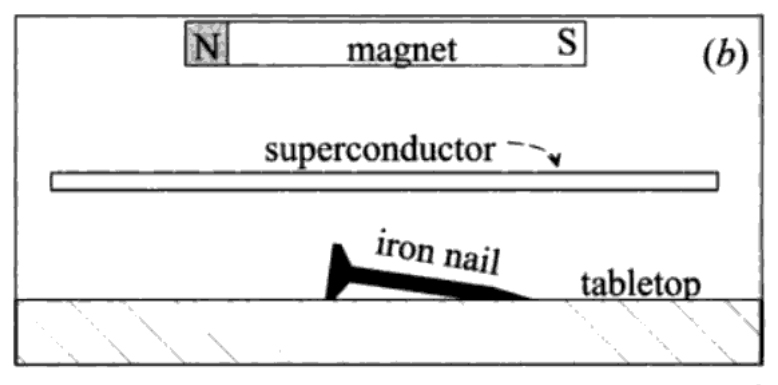
A magnetic field goes right through a material which is not superconducting: a magnet will attract an iron nail even if I interpose a sheet of normal metal in between, as shown in fig. 3, part (a). If I replace the normal metal by a superconducting sheet, as in part (b) of fig. XII-3, the magnetic field is stopped by it: the iron nail is not attracted by the magnet. If now I bring the magnet gradually closer to the superconducting sheet, I find that at a certain point the magnetic field apparently punches through the superconductor, because now the nail is attracted towards the magnet, as in part (c) of fig. 3.

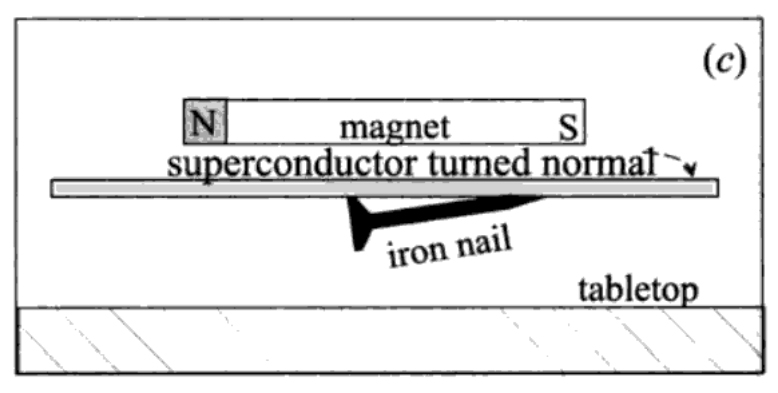FIGURE 3. (a) The field of a magnet goes right through a sheet of normal metal and acts on an iron nail on the other side, (b) The magnetic field is stopped by the superconducting sheet and does not appear on the other side; the nail lies quietly on the tabletop. (c) the magnet is brought closer to the sheet, until the field it sees is big enough to make it normal. The iron nail now feels the magnetic field and is attracted towards the sheet

QUESTION. Can you identify one essential detail which is missing in fig. 3?

ANSWER. Depending on what it is made of, the superconductor must be sitting in a bath of liquid air or liquid helium, because we have no materials which are superconducting at room temperature.

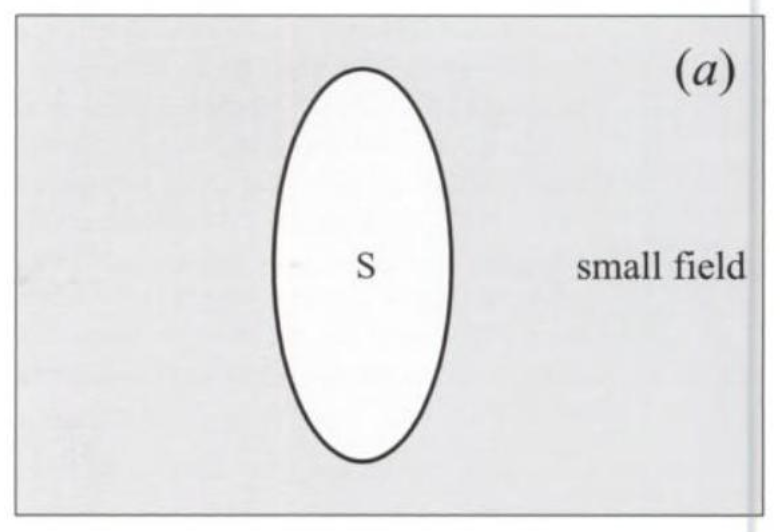
Further experimenting shows that the magnetic field punches through the superconductor if it is the LF type when its strength is equal to HM, which is also the field at which the material loses its superconductivity. I illustrate this effect in fig. 4. In part (a) of the figure, the field is less than HM, and cannot break into the superconductor (shown as an egg-shaped object in the picture). This is known as the Meissner effect, for Walther Meissner who in collaboration with R. Ochsenfeld discovered it. In part (b), the field is larger than HM, and becomes the same inside and outside the object, which is now normal. It is as if the superconductor tries to keep the field out because that is how it can remain superconducting, and the excluded field exerts a sort of pressure to get into the material. This pressure increases as the field increases, until finally the superconductor can no longer stand it. The field then punches its way in and kills the superconductivity.

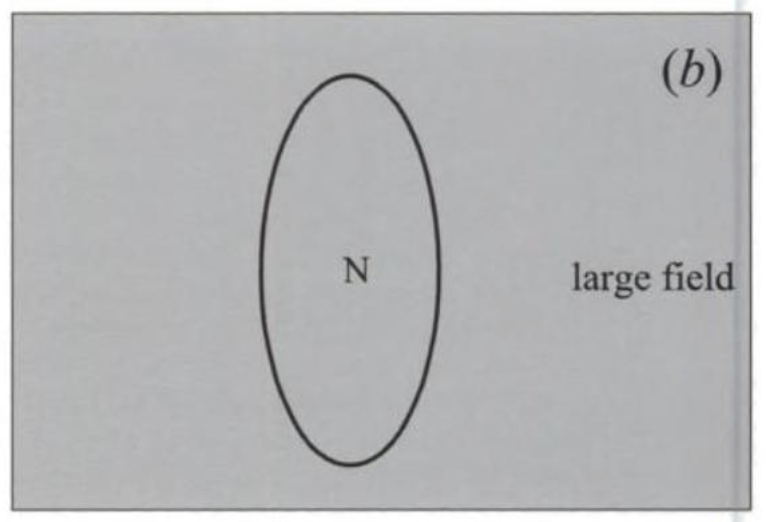FIGURE 4. A type I superconductor, shown as an egg-shaped object, (a) keeps a small field out, and (b) lets a large field in. The changeover is at the field HM, at which superconductivity ends. The state of the sample is indicated: S = superconducting, N = normal.

On the other hand, if the object is an HF superconductor, its behaviour is more cunning, so to speak, than that of the LF type. I illustrate it in fig. 5. In small fields, part (a), the HF type excludes the field just like the LF type. But at some medium field which is much less than HM for that material, it makes a compromise and lets a part of the field in, as shown in part (b) of the figure. The material then becomes an intimate mixture of superconducting and normal regions, and is said to be in the mixed state. As the field increases, it admits a larger and larger fraction of the field, and the normal fraction of the volume grows at the expense of the superconducting fraction. Finally at Hm the field inside and outside the material become equal, as shown in part (c), and the material becomes normal throughout its volume.

a)	b)	c)

Рис. 5. Сверхпроводник 2-го рода (в форме эллипсода вращения): а) не пропускает внутрь слабое магнитное поле; б) поле средней величины частично проникает внутрь такого сверхпроводника; в) когда поле достигает значения Bк для данного вещества, оно полностью проникает внутрь образца, который при этом переходит в нормальное состояние. S – сверхпроводящее cостояние, М – смешанное, N – нормальное

All HF superconductors show type II behaviour, and they are the ones which are mostly used in practical applications.

In a normal metal, I need to apply a voltage in order to send an electric current through it. In a superconductor, there is no resistance and a current can flow even without a voltage. If I start a current flowing in a superconducting ring, for example, it will continue for ever without diminishing, because there is no resistance. I call it a persistent current. This current going round the loop produces a magnetic field: it has a magnetic moment. This, like everything else in nature, is described by quantum mechanics. The magnetic moment is quantized. It can take only certain discrete values, and nothing in between. Measurements of this quantization give an unexpected result: the particles in the persistent current are not electrons acting singly and separately, but rather pairs of electrons acting as a unit. This is quite different from the normal state of the metal, in which the properties are those expected from electrons behaving singly. It is as if I made experiments with oxygen gas, and found that the results made sense only if the gas consisted not of single oxygen atoms, but rather of pairs of atoms bound together.

Some of the properties in the superconducting state of a material are the same as in the normal state, and others are quite different. The density and crystal structure do not change. The thermal conductivity and the specific heat, on the other hand, are quite different in the two states. The thermal conductivity does exactly the opposite of what we might expect from our understanding of normal metals. We saw there that a metal which is a good electrical conductor is also a good conductor of heat: copper for example. We might therefore expect that a superconductor would be also a super thermal conductor. Not so at all; the thermal conductivity of a metal in the superconducting state is smaller than what it is in the normal state. In the metal lead, for example, the thermal conductivity near 0 K in the superconducting state is about a million times smaller than in its normal state. The metal, although electrically a superconductor, becomes thermally an insulator. Since heat in metals is conducted primarily by electrons, it would appear that though the electrons in a superconductor carry an electric current with no resistance at all, they are strangely reluctant to carry a heat current. The specific heat in the superconducting state also is less than in the normal state.